正态分布和截断正态分布的差别

1. Normal Distribution 称为正态分布，也称为高斯分布，Truncated Normal Distribution 一般翻译为截断正态分布，也有称为截尾正态分布

2. 截断正态分布是截断分布 (Truncated Distribution) 的一种，那么截断分布是什么？截断分布是指，限制变量 x 取值范围 (scope) 的一种分布。例如，限制 x 取值在 0 到 50 之间，即 {0<x<50}。因此，根据限制条件的不同，截断分布可以分为： 2.1 限制取值上限，例如，负无穷 < x<50 2.2 限制取值下限，例如，0 需要注意的是，任何密度函数曲线下方的面积是 1。因此，截断，并不意味着直接把原始密度函数两边去掉一部分；而是，截断后概率密度函数曲线会有一些变化，使得总面积仍然为 1。 4. 截断之后概率密度函数如何重新计算？ 假设 X 原来服从正太分布，那么限制 x 的取值在（a，b）范围内之后，X 的概率密度函数，可以用下面公式计算：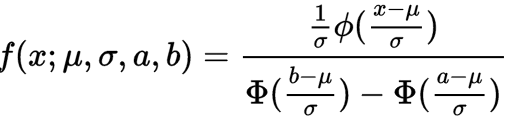

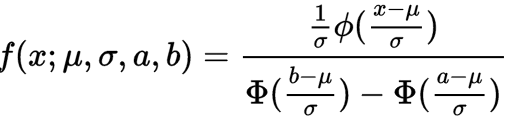
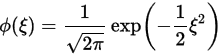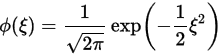显然，对于（a，b）范围之外的那些 x，对应的概率密度 f=0。 上式中，小写的 φ，表示： 是标准正态分布。 大写的 Φ，是标准正态分布的累积分布 (cumulative distribution function)—— 某个值左边的面积总和。

5. 应用

截断正态分布在模型参数初始化时比较好，例如，Tensorflow 提供了 truncated_normal 函数，自动截断超过 2 倍标准差的样本点。